Многим пользователям Сети не дает покоя задача, предназначенная для учеников начальной школы в Китае. Несмотря на кажущуюся простоту, многие так и не смогли найти решение.
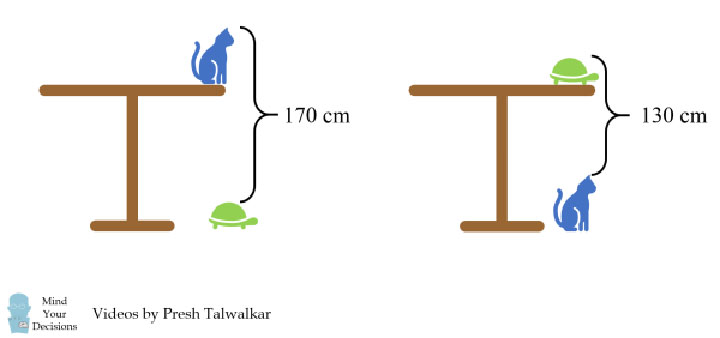
Задание звучит следующим образом: «Найдите высоту стола, зная, что расстояние между головой кота на столе и головой черепахи на земле составляет 170 см, а расстояние между головой черепахи на столе и головой кота на земле составляет 130 см».
Итак, какая высота стола?
Решение

После того, как эта задача стала вирусной, эксперты попытались найти правильное решение, учитывая тысячи гипотез пользователей. Решить задачу можно двумя способами — алгебраическим и визуальным.
Алгебраический способ
Посмотрев на левую часть рисунка, можно составить следующее уравнение:
высота кота + высота стола — высота черепахи = 170
Аналогично с правой частью картинки:
высота черепахи + высота стола — высота кота = 130
По правилам алгебры, два уравнения могут быть объединены вместе, отсюда получаем:
высота кота + высота стола — высота черепахи + высота черепахи + высота стола — высота кота = 170 + 130
исходя из этого уравнения, мы можем аннулировать высоту кота и высоту черепахи, поскольку они равны и имеют разные знаки в итоговом уравнении, отсюда получаем:
высота стола + высота стола = 300
или же
2(высота стола) = 300
отсюда легко получить итоговую высоту стола: высота стола = 300/2 = 150 см
Визуальный способ
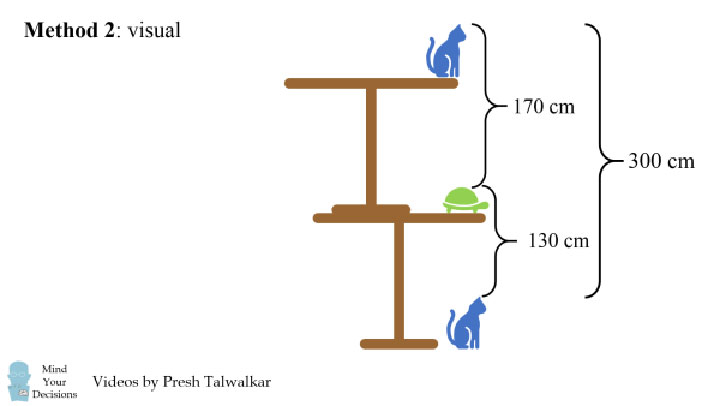
Второй способ решить задачу — визуализировать ее. Совместите левое и правое изображение, спустите скобку на высоту кота и визуально станет понятно, что сумма высот 130 и 170 см точно соответствует высоте двух столов без животных (300 см). Поделив это значение на два, можно получить высоту одного стола.
А вам удалось найти решение?



